Forecasting Intermittent Demand

Introduction

Intermittent demand occurs when products or services have irregular purchase patterns with frequent zero-value periods. This is common in retail, spare parts inventory, and specialty products where demand is irregular rather than continuous. Forecasting these patterns accurately is essential for optimizing stock levels, reducing costs, and preventing stockouts. TimeGPT excels at intermittent demand forecasting by capturing complex patterns that traditional statistical methods miss. This tutorial demonstrates TimeGPT’s capabilities using the M5 dataset of food sales, including exogenous variables like pricing and promotional events that influence purchasing behavior.

What You’ll Learn

How to prepare and analyze intermittent demand data
How to leverage exogenous variables for better predictions
How to use log transforms to ensure realistic forecasts
How TimeGPT compares to specialized intermittent demand models

The methods shown here apply broadly to inventory management and retail forecasting challenges. For getting started with TimeGPT, see our quickstart guide.

How to Use TimeGPT to Forecast Intermittent Demand

Step 1: Environment Setup

Start by importing the required packages for this tutorial and create an instance of NixtlaClient.

import pandas as pd
import numpy as np

from nixtla import NixtlaClient
from utilsforecast.losses import mae
from utilsforecast.evaluation import evaluate

nixtla_client = NixtlaClient(api_key='my_api_key_provided_by_nixtla')

Step 2: Load and Visualize the Dataset

Load the dataset from the M5 dataset and convert the ds column to a datetime object:

df = pd.read_csv("https://raw.githubusercontent.com/Nixtla/transfer-learning-time-series/main/datasets/m5_sales_exog_small.csv")
df['ds'] = pd.to_datetime(df['ds'])
df.head()

unique_id	ds	y	sell_price
FOODS_1_001	2011-01-29	3	2.0
FOODS_1_001	2011-01-30	0	2.0
FOODS_1_001	2011-01-31	0	2.0
FOODS_1_001	2011-02-01	1	2.0
FOODS_1_001	2011-02-02	4	2.0

Visualize the dataset using the plot method:

nixtla_client.plot(
    df,
    max_insample_length=365,
)

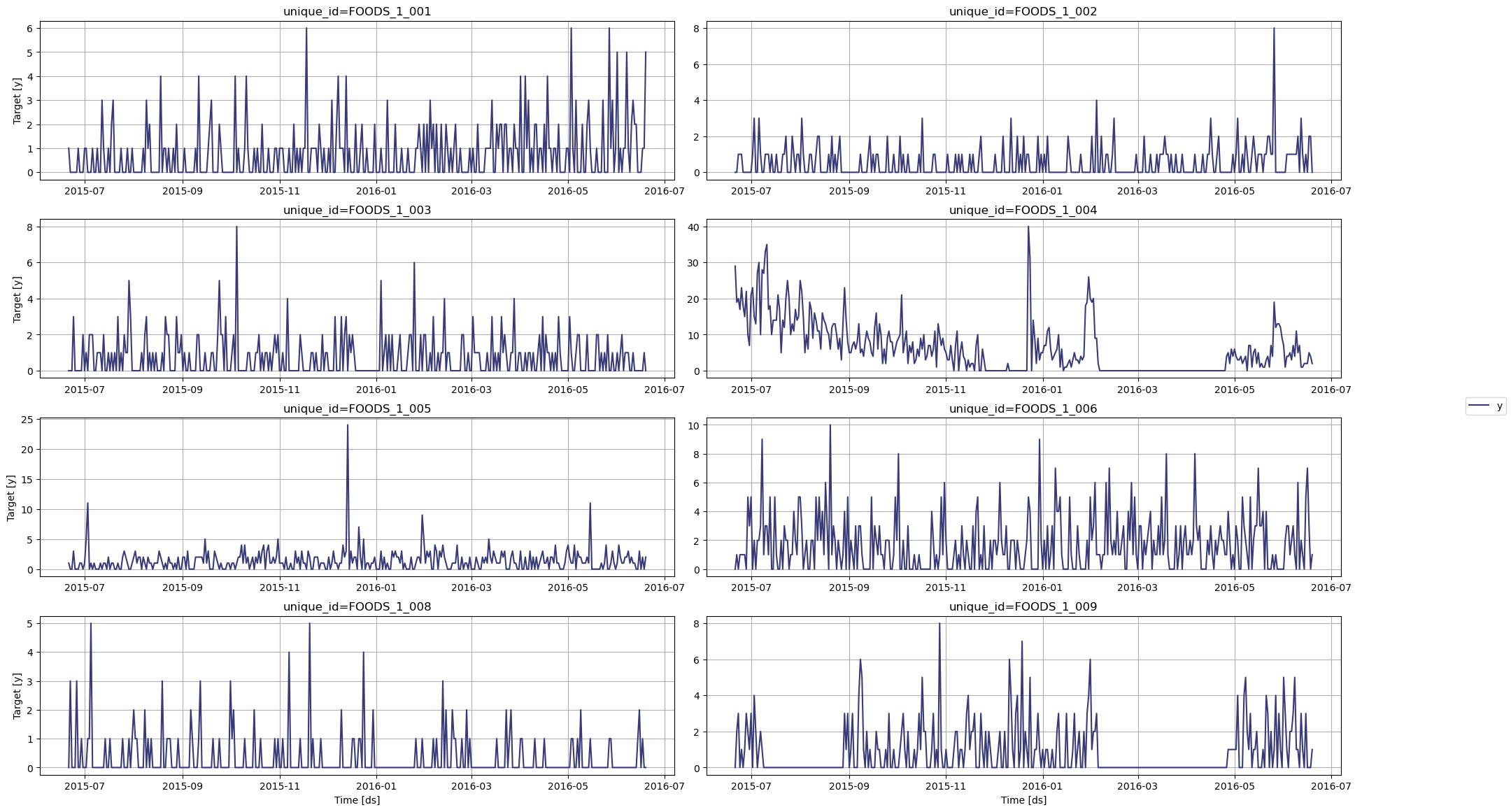
Figure 1: Visualization of intermittent demand data

In the figure above, we can see the intermittent nature of this dataset, with many periods with zero demand. Now, let’s use TimeGPT to forecast the demand of each product.

Step 3: Transform the Data

To avoid getting negative predictions coming from the model, we use a log transformation on the data. That way, the model will be forced to predict only positive values. Note that due to the presence of zeros in our dataset, we add one to all points before taking the log.

df_transformed = df.copy()
df_transformed['y'] = np.log(df_transformed['y'] + 1)

Now, let’s keep the last 28 time steps for the test set and use the rest as input to the model.

test_df = df_transformed.groupby('unique_id').tail(28)
input_df = df_transformed.drop(test_df.index).reset_index(drop=True)

Step 4: Forecast with TimeGPT

Forecast with TimeGPT using the forecast method:

fcst_df = nixtla_client.forecast(
    df=input_df,
    h=28,
    level=[80],
    finetune_steps=10,               # Learn more about fine-tuning: /forecasting/fine-tuning/steps
    finetune_loss='mae',
    model='timegpt-1-long-horizon',  # For long-horizon forecasting: /forecasting/model-version/longhorizon_model
    time_col='ds',
    target_col='y',
    id_col='unique_id'
)

INFO:nixtla.nixtla_client:Validating inputs...
INFO:nixtla.nixtla_client:Preprocessing dataframes...
INFO:nixtla.nixtla_client:Inferred freq: D
INFO:nixtla.nixtla_client:Calling Forecast Endpoint...

Great! We now have predictions. However, those predictions are transformed, so we need to inverse the transformation to get back to the original scale. Therefore, we take the exponential and subtract one from each data point.

cols = [col for col in fcst_df.columns if col not in ['ds', 'unique_id']]
fcst_df[cols] = np.exp(fcst_df[cols]) - 1
fcst_df.head()

	unique_id	ds	TimeGPT	TimeGPT-lo-80	TimeGPT-hi-80
0	FOODS_1_001	2016-05-23	0.286841	-0.267101	1.259465
1	FOODS_1_001	2016-05-24	0.320482	-0.241236	1.298046
2	FOODS_1_001	2016-05-25	0.287392	-0.362250	1.598791
3	FOODS_1_001	2016-05-26	0.295326	-0.145489	0.963542
4	FOODS_1_001	2016-05-27	0.315868	-0.166516	1.077437

Step 5: Evaluate the Forecasts

Before measuring the performance metric, let’s plot the predictions against the actual values.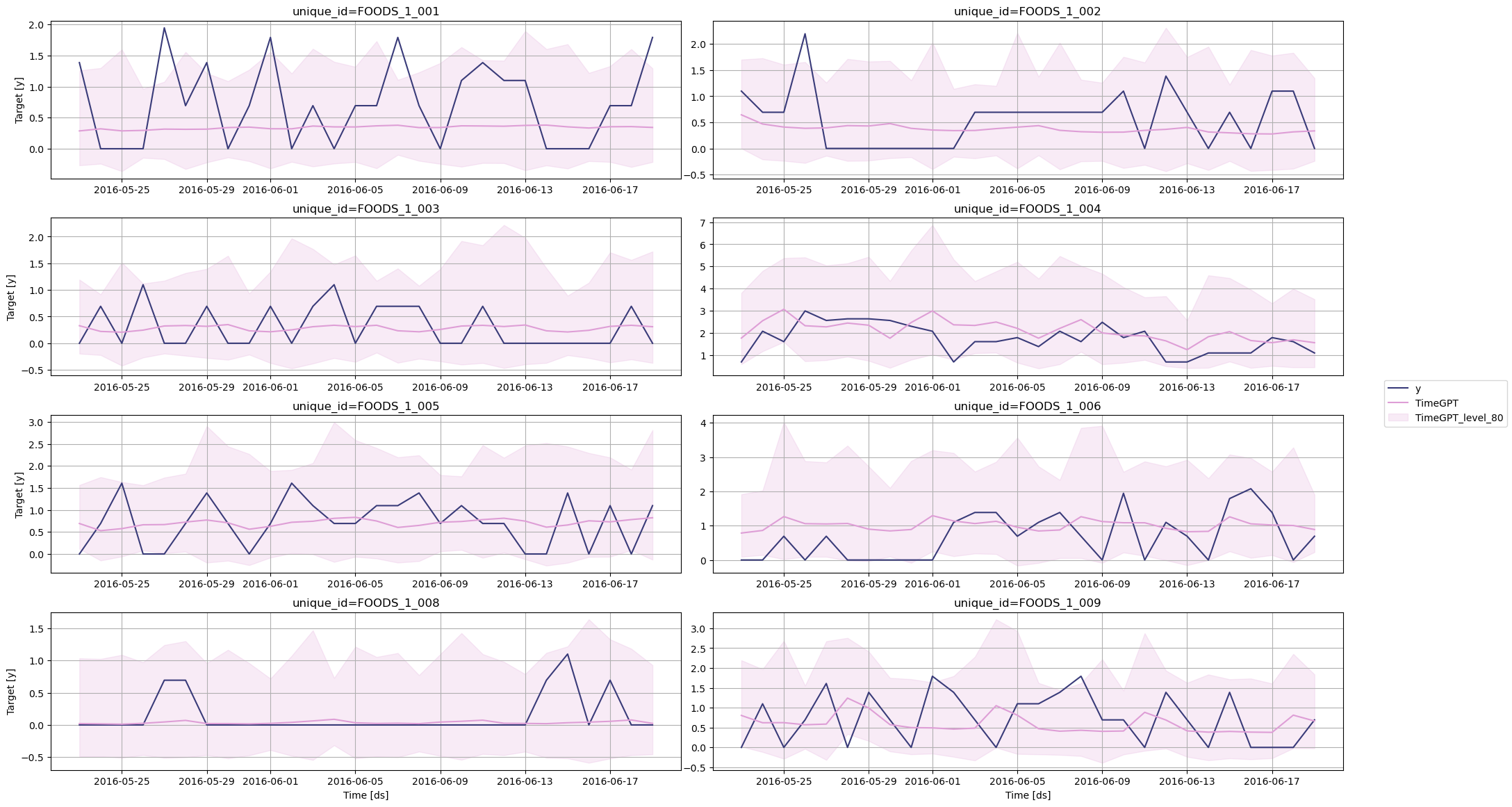

nixtla_client.plot(
    test_df,
    fcst_df,
    models=['TimeGPT'],
    level=[80],
    time_col='ds',
    target_col='y'
)

Figure 2: Visualization of the predictions against the actual values

Finally, we can measure the mean absolute error (MAE) of the model. Learn more about evaluation metrics in our documentation.

# Compute MAE
test_df = pd.merge(test_df, fcst_df, how='left', on=['unique_id', 'ds'])
evaluation = evaluate(
    test_df,
    metrics=[mae],
    models=['TimeGPT'],
    target_col='y',
    id_col='unique_id'
)
average_metrics = evaluation.groupby('metric')['TimeGPT'].mean()
average_metrics

metric
mae    0.492559

Step 6: Compare with Statistical Models

The library statsforecast by Nixtla provides a suite of statistical models specifically built for intermittent forecasting, such as Croston, IMAPA and TSB. Let’s use these models and see how they perform against TimeGPT.

from statsforecast import StatsForecast
from statsforecast.models import CrostonClassic, CrostonOptimized, IMAPA, TSB

sf = StatsForecast(
    models=[CrostonClassic(), CrostonOptimized(), IMAPA(), TSB(0.1, 0.1)],
    freq='D',
    n_jobs=-1
)

Then, we can fit the models on our data.

sf.fit(df=input_df)
sf_preds = sf.predict(h=28)

Again, we need to inverse the transformation. Remember that the training data was previously transformed using the log function.

cols = [col for col in sf_preds.columns if col not in ['ds', 'unique_id']]
sf_preds[cols] = np.exp(sf_preds[cols]) - 1
sf_preds.head()

	unique_id	ds	CrostonClassic	CrostonOptimized	IMAPA	TSB
0	FOODS_1_001	2016-05-23	0.599093	0.599093	0.445779	0.396258
1	FOODS_1_001	2016-05-24	0.599093	0.599093	0.445779	0.396258
2	FOODS_1_001	2016-05-25	0.599093	0.599093	0.445779	0.396258
3	FOODS_1_001	2016-05-26	0.599093	0.599093	0.445779	0.396258
4	FOODS_1_001	2016-05-27	0.599093	0.599093	0.445779	0.396258

Now, let’s combine the predictions from all methods and see which performs best.

test_df = pd.merge(test_df, sf_preds, 'left', ['unique_id', 'ds'])
test_df.head()

	unique_id	ds	y	sell_price	TimeGPT	TimeGPT-lo-80	TimeGPT-hi-80	CrostonClassic	CrostonOptimized	IMAPA	TSB
0	FOODS_1_001	2016-05-23	1.386294	2.24	0.286841	-0.267101	1.259465	0.599093	0.599093	0.445779	0.396258
1	FOODS_1_001	2016-05-24	0.000000	2.24	0.320482	-0.241236	1.298046	0.599093	0.599093	0.445779	0.396258
2	FOODS_1_001	2016-05-25	0.000000	2.24	0.287392	-0.362250	1.598791	0.599093	0.599093	0.445779	0.396258
3	FOODS_1_001	2016-05-26	0.000000	2.24	0.295326	-0.145489	0.963542	0.599093	0.599093	0.445779	0.396258
4	FOODS_1_001	2016-05-27	1.945910	2.24	0.315868	-0.166516	1.077437	0.599093	0.599093	0.445779	0.396258

statistical_models = ["CrostonClassic", "CrostonOptimized", "IMAPA", "TSB"]
evaluation = evaluate(
    test_df,
    metrics=[mae],
    models=["TimeGPT"] + statistical_models,
    target_col="y",
    id_col='unique_id'
)

average_metrics = evaluation.groupby('metric')[[
    "TimeGPT"] + statistical_models].mean()
average_metrics

metric	TimeGPT	CrostonClassic	CrostonOptimized	IMAPA	TSB
mae	0.492559	0.564563	0.580922	0.571943	0.567178

In the table above, we can see that TimeGPT achieves the lowest MAE, achieving a 12.8% improvement over the best performing statistical model. These results demonstrate TimeGPT’s strong performance without additional features. We can further improve accuracy by incorporating exogenous variables, a capability TimeGPT supports but traditional statistical models do not.

Step 7: Use Exogenous Variables

To forecast with exogenous variables, we need to specify their future values over the forecast horizon. Therefore, let’s simply take the types of events, as those dates are known in advance. You can also explore using date features and holidays as exogenous variables.

# Include holiday/event data as exogenous features
exog_cols = ['event_type_Cultural', 'event_type_National', 'event_type_Religious', 'event_type_Sporting']
futr_exog_df = test_df[['unique_id', 'ds'] + exog_cols]
futr_exog_df.head()

	unique_id	ds
0	FOODS_1_001	2016-05-23
1	FOODS_1_001	2016-05-24
2	FOODS_1_001	2016-05-25
3	FOODS_1_001	2016-05-26
4	FOODS_1_001	2016-05-27

Then, we simply call the forecast method and pass the futr_exog_df in the X_df parameter.

fcst_df = nixtla_client.forecast(
    df=input_df,
    X_df=futr_exog_df,
    h=28,
    level=[80],                        # Generate a 80% confidence interval
    finetune_steps=10,                 # Specify the number of steps for fine-tuning
    finetune_loss='mae',               # Use the MAE as the loss function for fine-tuning
    model='timegpt-1-long-horizon',    # Use the model for long-horizon forecasting
    time_col='ds',
    target_col='y',
    id_col='unique_id'
)

INFO:nixtla.nixtla_client:Validating inputs...
INFO:nixtla.nixtla_client:Preprocessing dataframes...
INFO:nixtla.nixtla_client:Inferred freq: D
INFO:nixtla.nixtla_client:Using the following exogenous variables: event_type_Cultural, event_type_National, event_type_Religious, event_type_Sporting
INFO:nixtla.nixtla_client:Calling Forecast Endpoint...

Great! Remember that the predictions are transformed, so we have to inverse the transformation again.

fcst_df.rename(columns={'TimeGPT': 'TimeGPT_ex'}, inplace=True)

cols = [col for col in fcst_df.columns if col not in ['ds', 'unique_id']]
fcst_df[cols] = np.exp(fcst_df[cols]) - 1

fcst_df.head()

	unique_id	ds	TimeGPT_ex	TimeGPT-lo-80	TimeGPT-hi-80
0	FOODS_1_001	2016-05-23	0.281922	-0.269902	1.250828
1	FOODS_1_001	2016-05-24	0.313774	-0.245091	1.286372
2	FOODS_1_001	2016-05-25	0.285639	-0.363119	1.595252
3	FOODS_1_001	2016-05-26	0.295037	-0.145679	0.963104
4	FOODS_1_001	2016-05-27	0.315484	-0.166760	1.076830

Finally, let’s evaluate the performance of TimeGPT with exogenous features.

test_df['TimeGPT_ex'] = fcst_df['TimeGPT_ex'].values
test_df.head()

	unique_id	ds	y	sell_price	TimeGPT	TimeGPT-lo-80	TimeGPT-hi-80	CrostonClassic	CrostonOptimized	IMAPA	TSB	TimeGPT_ex
0	FOODS_1_001	2016-05-23	1.386294	2.24	0.286841	-0.267101	1.259465	0.599093	0.599093	0.445779	0.396258	0.281922
1	FOODS_1_001	2016-05-24	0.000000	2.24	0.320482	-0.241236	1.298046	0.599093	0.599093	0.445779	0.396258	0.313774
2	FOODS_1_001	2016-05-25	0.000000	2.24	0.287392	-0.362250	1.598791	0.599093	0.599093	0.445779	0.396258	0.285639
3	FOODS_1_001	2016-05-26	0.000000	2.24	0.295326	-0.145489	0.963542	0.599093	0.599093	0.445779	0.396258	0.295037
4	FOODS_1_001	2016-05-27	1.945910	2.24	0.315868	-0.166516	1.077437	0.599093	0.599093	0.445779	0.396258	0.315484

evaluation = evaluate(
    test_df,
    metrics=[mae],
    models=["TimeGPT"] + statistical_models + ["TimeGPT_ex"],
    target_col="y",
    id_col='unique_id'
)

average_metrics = (
    evaluation.groupby('metric')[["TimeGPT"] + statistical_models + ["TimeGPT_ex"]]
).mean()
average_metrics

metric	TimeGPT	CrostonClassic	CrostonOptimized	IMAPA	TSB	TimeGPT_ex
mae	0.492559	0.564563	0.580922	0.571943	0.567178	0.485352

From the table above, we can see that using exogenous features improved the performance of TimeGPT. Now, it represents a 14% improvement over the best statistical model.

Conclusion

TimeGPT provides a robust solution for forecasting intermittent demand:

~14% MAE improvement over specialized models
Supports exogenous features for enhanced accuracy

By leveraging TimeGPT and combining both internal series patterns and external factors, organizations can achieve more reliable forecasts even for challenging intermittent demands.

Next Steps

Explore other use cases with TimeGPT
Learn about probabilistic forecasting with prediction intervals
Scale your forecasts with distributed computing
Fine-tune models with custom loss functions

INTRODUCTION

SETUP

DATA REQUIREMENTS

FORECASTING

ANOMALY DETECTION

USE CASES

REFERENCE

About

Introduction

What You’ll Learn

How to Use TimeGPT to Forecast Intermittent Demand

Step 1: Environment Setup

Step 2: Load and Visualize the Dataset

Step 3: Transform the Data

Step 4: Forecast with TimeGPT

Step 5: Evaluate the Forecasts

Step 6: Compare with Statistical Models

Step 7: Use Exogenous Variables

Conclusion

Next Steps

INTRODUCTION

SETUP

DATA REQUIREMENTS

FORECASTING

ANOMALY DETECTION

USE CASES

REFERENCE

About

​Introduction

​What You’ll Learn

​How to Use TimeGPT to Forecast Intermittent Demand

​Step 1: Environment Setup

​Step 2: Load and Visualize the Dataset

​Step 3: Transform the Data

​Step 4: Forecast with TimeGPT

​Step 5: Evaluate the Forecasts

​Step 6: Compare with Statistical Models

​Step 7: Use Exogenous Variables

​Conclusion

​Next Steps

Introduction

What You’ll Learn

How to Use TimeGPT to Forecast Intermittent Demand

Step 1: Environment Setup

Step 2: Load and Visualize the Dataset

Step 3: Transform the Data

Step 4: Forecast with TimeGPT

Step 5: Evaluate the Forecasts

Step 6: Compare with Statistical Models

Step 7: Use Exogenous Variables

Conclusion

Next Steps